Symmetries between sine and cosine

Geometry

We must start with the most basic definition.

Lemma 1: Basic definitions in right triangle

In a right triangle, given angle \(\theta\), \(\sin \theta = \frac{\text{opposite}}{\text{hypotenuse}}\) and \(\cos \theta = \frac{\text{adjacent}}{\text{hypotenuse}}\)

But it’s definitely best to visualize:

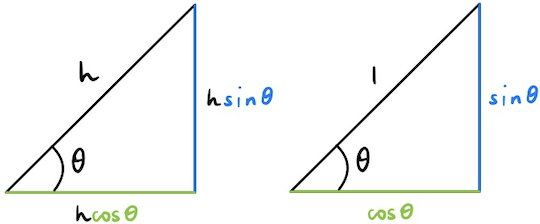
From the definitions, we get that the green side is \(h\cos \theta\) because \(\cos \theta = \frac{\text{adjacent}}{\text{hypotenuse}} \implies \text{adjacent} = h\cos \theta\). Similarly, the blue side is \(h\sin \theta\). Letting \(h=1\), the adjacent side is just \(\cos \theta\), and the opposite side is \(\sin \theta\). With this setup, we can show Lemma 2.

Lemma 2: 90° separation

\(\cos \theta = \sin(\frac{\pi}{2} - \theta)\) and \(\sin \theta = \cos(\frac{\pi}{2} - \theta)\) for arbitrary \(\theta\)

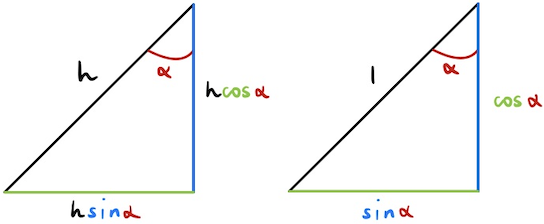
Proof. Consider \(\alpha=\frac{\pi}{2}-\theta\). In the triangle with hypotenuse 1, the green side is \(\cos \theta = \frac{\text{adjacent}}{1}\). It is also \(\sin \alpha = \frac{\text{opposite}}{1}\). Hence, \(\cos \theta = \sin(\frac{\pi}{2} - \theta)\). Similar reasoning holds for the latter identity and for arbitrary \(h\).

Here’s a Desmos graph where you can see the identity for yourself: ¹

Back to Lemma 1, why should the basic definition be limited to a static right triangle? What about a dynamic right triangle, perhaps one like this: ²

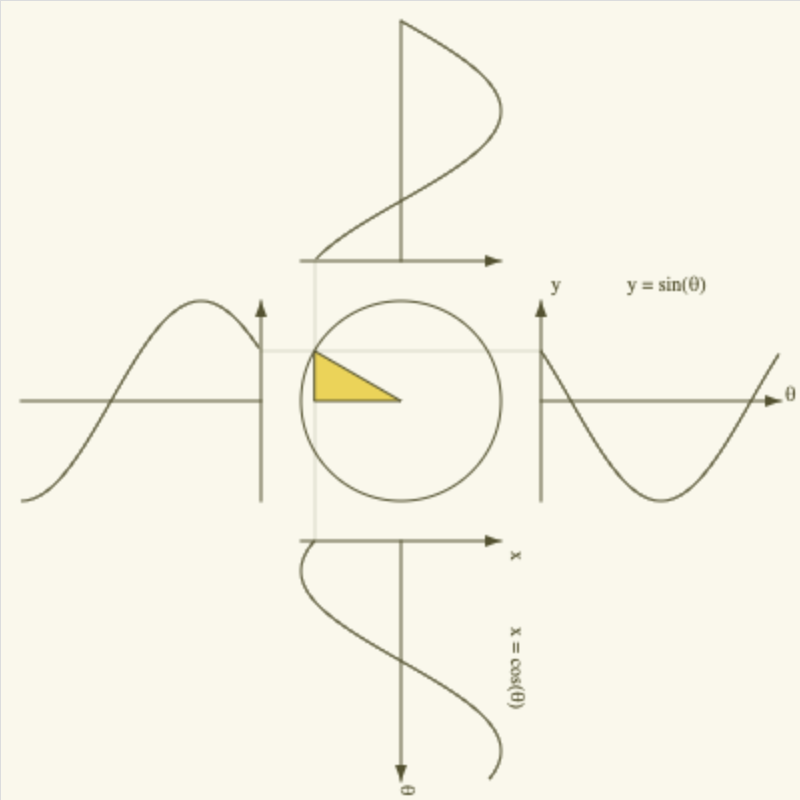
In this graph, the x coordinates always involve \(\cos \theta\), and the y coordinates always involve \(\sin \theta\). Thinking of the black line as a vector ³, we see that to get the horizontal component of the vector, we multiply its length by \(\cos \theta\). To get its vertical component, we multiply its length by \(\sin \theta\). In other words, \(\cos \theta\) projects to \(x\), and \(\sin \theta\) projects to \(y\).

This applies to the graph of a circle as well. Note that, again, \(x\) always goes with \(\cos \theta\), and \(y\) always goes with \(\sin \theta\).

To make this idea even more clear, you should take a look at this unit circle animation on Khan Academy.

Algebra

There is an algebraic symmetry that is, in my opinion, as beautiful as the symmetries above. This symmetry also allows us to prove \(e^{ix} = \cos x + i\sin x\) for any \(x\).

Lemma 3: Sine and cosine series expansions

\(\cos x = 1 - \frac{x^2}{2} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots\), and \(\sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots\) ⁴

Proof. Consider that the Taylor series ⁵ expansion of \(f(x)\) about the point \(a\) is \(f(a)+f'(a)(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \frac{f'''(a)}{3!}(x-a)^3 + \cdots + \frac{f^{(n)}(a)}{n!}(x-a)^n + \cdots\)

The Maclaurin expansion is the Taylor series centered at \(a=0\), so the Maclaurin expansion of \(f(x)\) is \(f(0) + f'(0)x + \frac{f''(0)}{2!}x^2 + \frac{f'''(0)}{3!}x^3 + \cdots + \frac{f^{(n)}(0)}{n!}x^n + \cdots\)

Let \(f(x) = \cos x\). We know that ⁶

\[\begin{matrix} f(x) & = & \cos x\\ f'(x) & = & -\sin x\\ f''(x) & = & -\cos x\\ f'''(x) & = & \sin x\\ f''''(x) & = & \cos x\\ \vdots & \vdots & \vdots \end{matrix}\]

Using that \(\cos(0) = 1\) and \(\sin(0) = 0\), we have that the first few terms of the Maclaurin series are \(1 + 0x -\frac{x^2}{2} + 0x^3 + \frac{x^4}{4!}\). Now, we write the pattern:

\[\cos x = \sum_{n=0}^{\infty} \frac{(-1)^n}{2n!} x^{2n}\]

Any odd power will have \(\sin(0)=0\) and so can be ignored. Hence, we use only the even numbers \(2n\) in our summation. Using that \(f(x)=\cos x\) and \(f''(x) = -\cos x\), we note that the signs alternate each (even) term, so we also have \((-1)^n\) in the summation.

Similar reasoning holds for \(\sin x = \sum_{n=0}^{\infty} \frac{(-1)^n}{(2n+1)!}x^{2n+1}\).

Lastly, there are also two trigonometric identities that I have always found interesting, in terms of symmetry.

Lemma 4: Angle sum and difference identities

\[\sin(\alpha + \beta) = \sin(\alpha) \cos(\beta) + \cos(\alpha) \sin(\beta)\] \[\sin(\alpha - \beta) = \sin(\alpha) \cos(\beta) - \cos(\alpha) \sin(\beta)\] \[\cos(\alpha + \beta) = \cos(\alpha) \cos(\beta) - \sin(\alpha) \sin(\beta)\] \[\cos(\alpha - \beta) = \cos(\alpha) \cos(\beta) + \sin(\alpha) \sin(\beta)\]

I won’t prove these identities here, but I will write about the symmetries. Note that the \(\sin\) identities have matching signs; that is, if there is a \(+\) on the left side, there’s a \(+\) on the right side. However, the multiplications are mismatched in that \(\sin\) is multiplied by \(\cos\) and vice versa.

On the other hand, the \(\cos\) identities have matching multiplication in that \(\cos\) multiplies \(\cos\), and \(\sin\) multiplies \(\sin\). The signs, however, are mismatched.