Binary

Before we talk about binary, let’s first go over the base-10 decimal system.

Decimal (base-10)

You might know that we count in base-10, the decimal counting system. What does that mean?

Base-10 means there are 10 symbols that we use to count. These symbols are \(\{0, 1, 2, 3, 4, 5, 6, 7, 8, 9\}\).

How does our number system work? For decimal numbers, we have a ones place, a tens place, a hundreds place, and a thousands place. 1, 10, 100, and 1000 are all powers of 10: \(10^0,\\; 10^1,\\; 10^2,\\; 10^3\), respectively. In this system, 1337 is represented as \((1\times 10^3) + (3\times 10^2) + (3\times 10^1) + (7\times 10^0)\). That is, there is a 1 in the thousands place, a 3 in the hundreds place and in the tens place, and a 7 in the ones place. Decimals are represented in the same way. 2.1337 is \((2 \times 10 ^ 0) + (1\times10^{-1})+(3\times10^{-2})+(3\times 10^{-3})+(7\times 10^{-4})\).

This is why we carry numbers when adding. If we do \(1337 + 1337\), \((7\times 10^0)+(7\times 10^0)=14=(1\times 10^1)+(4\times 10^0)\), so we can put a 4 in the ones place and carry the \(1\) over to the tens place.

Why is this useful? Consider this question: What is the largest 3-digit integer? Clearly, it’s 999, which comes from putting the greatest symbol into the 3 slots we have. But what if I ask what the largest 8-digit integer is? You would have to write eight 9’s. Surely, there’s a simpler, more general way to write the answer?

Consider the number that is 1 greater, which is a 1 followed by 8 zeroes, \(1\underbrace{00...0}_{8}\). What is the value of that number?

☣ A very common mistake would be to say the highest place value in \(1\underbrace{000...0}_{8}\) is \(10^9\) because there are 9 digits. Here, we zero-index (start counting from 0).

Exercise: Write out the place values of each digit to make sure you understand how the \(1\) has value \(1 \times 10^8\).

Then the largest 8-digit integer is \(10^8-1=99999999\). Now, you also know that the largest 32-digit integer is \(10^{32}-1\) and so on. Let’s see an example of how this is useful.

Binary (base-2)

You’re reading this on a computer right now. Behind the scenes of any computer is code. And code consists of variables and variable types, such as int, float, and double.

Let’s focus on int. In the C programming language, an unsigned int is a 32-bit data type that stores positive integers and 0. What’s the greatest number that can be stored in an unsigned int?

Let’s now talk about binary, though you should have a pretty good understanding of it by now. “bi-“ means two, so there are only two symbols in binary: 0 and 1. Here’s how we count from \(0_{10}\) to \(7_{10}\) in binary: 0, 1, 10, 11, 100, 101, 110, 111.

This follows the same pattern as base-10. In base-10, if we see a 9 and add 1 to it, we reset it to 0 and carry over a 1. In binary, we do the same but whenever we see a 1 and add 1 to it since we have only 2 symbols.

Also note that \(111_2\) is \((1\times 2^2) + (1\times 2^1) + (1\times 2^0) = 7_{10}\).

\(111_2\) is the greatest 3-bit number: does this match up with what we learned before? The greatest 3-bit number should be \(2^3-1=7_{10}\), so it works! Addition and subtraction work the same way as in base-10. There’s a special trick for binary subtraction called 2’s complement. If you’re interested in that, read more about it here.

Then the greatest number that can be stored in an unsigned int is \(2^{32}-1 = 4294967295_{10}\).

Proof. The greatest 32-digit base-2 value is \(\underbrace{111...1}_{32}\).

Consider \(\underbrace{100...0}_{33}\), the number that is 1 greater.

Its value is \(1 \times 2^{32}\), hence \(\underbrace{111...1}_{32} = 2^{32} - 1\). \(\blacksquare\)

Hexadecimal (base-16)

An alternative representation of \(\underbrace{111...1}_{32}\) is 0xFFFFFFFF. The 0x prefix indicates hexadecimal, which is a base-16 counting system with symbols [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F]. Each hex digit represents 4 binary digits because \(2^4=16\).

Application

Why is this important?

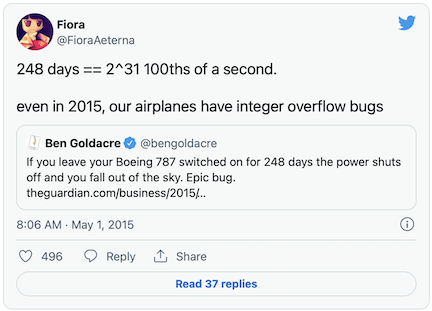
Now you understand why Boeing 787 airplanes have this issue! It’s a simple case of integer overflow. Computer memory is aligned in chunks, and in C and other programming languages, an unsigned int is specified to take up 32 bits or \(\frac{32}{8}=4\) bytes, no matter how large or small.

takes up the same amount of space as does \(1_{10} = \underbrace{000...1}_{32}\).

Why? If memory weren’t aligned, such that each number does not have leading zeroes to fill up the allocated 32 bits, how could you know where one number ends and another begins?

Overflow

Lastly, what would happen if we were to add 1 to the unsigned int \(\underbrace{111...1}_{32}\), having just learned that

an unsigned int cannot have a 33^rd bit? The ALU of the computer adds 1, but the 33^rd 1 is discarded since it doesn’t fit, leaving just \(\underbrace{000...0}_{32} = 0\), an overflow error. Yikes.

#include <stdio.h>

int main() {
    unsigned int int_max = 0xFFFFFFFF; // F == 1111 == 15 in base-10
    // hence 0xFFFFFFFF is 32 binary bits, all 1's
    printf("%u\n", int_max);
    printf("%u\n", int_max + 1);
}

4294967295
0